js二叉树的遍历算法
二叉树的概念
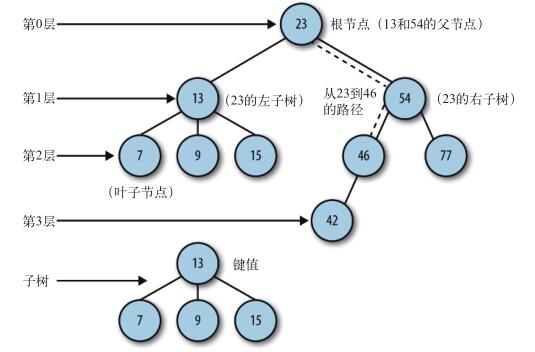
二叉树是非常重要的数据结构,其中一棵树最上面的点称为根节点,如果一个节点下面连接多个节点,那么该节点称为父节点,下面的节点称为子节点,二叉树的每一个节点最多有2个子节点,一个节点子节点的个数称为度,二叉树每个节点的度只能是0,1,2中的一个,度为0的节点称为叶节点。
js二叉树的实现
用JS实现二叉树数据结构, 完成遍历、查找最大/小值、查找特定值以及删除节点的操作。
//定义节点
class Node {
constructor(data){
this.root = this;
this.data = data;
this.left = null;
this.right = null
}
}
//创建二叉搜索树(BST))
class BinarySearchTree {
constructor(){
this.root = null
}
//插入节点
insert(data){
const newNode = new Node(data);
const insertNode = (node,newNode) => {
if (newNode.data < node.data){
if(node.left === null){
node.left = newNode
}else {
insertNode(node.left,newNode)
}
}else {
if(node.right === null){
node.right = newNode
}else{
insertNode(node.right,newNode)
}
}
};
if(!this.root){
this.root = newNode
}else {
insertNode(this.root,newNode)
}
}
//中序遍历
inOrder(){
let backs = [];
const inOrderNode = (node,callback) => {
if(node !== null){
inOrderNode(node.left,callback);
backs.push(callback(node.data));
inOrderNode(node.right,callback)
}
};
inOrderNode(this.root,callback);
function callback(v){
return v
}
return backs
}
//前序遍历
preOrder(){
let backs = [];
const preOrderNode = (node,callback) => {
if(node !== null){
backs.push(callback(node.data));
preOrderNode(node.left,callback);
preOrderNode(node.right,callback)
}
};
preOrderNode(this.root,callback);
function callback(v){
return v
}
return backs
}
//后序遍历
postOrder(){
let backs = [];
const postOrderNode = (node,callback) => {
if(node !== null){
postOrderNode(node.left,callback);
postOrderNode(node.right,callback);
backs.push(callback(node.data))
}
};
postOrderNode(this.root,callback);
function callback(v){
return v
}
return backs
}
//查找最小值
getMin(node){
const minNode = node => {
return node? (node.left? minNode(node.left):node):null
};
return minNode( node || this.root)
}
//查找最大值
getMax(node){
const minNode = node => {
return node? (node.right? minNode(node.right):node):null
};
return minNode(node || this.root)
}
//查找特定值
find(data){
const findNode = (node,data) => {
if(node===null) return false;
if(node.data===data) return node;
return findNode((data < node.data)? node.left: node.right,data)
};
return findNode(this.root,data)
}
//删除节点
remove(data){
const removeNode = (node,data) => {
if(node === null) return null;
if(node.data === data){
if(node.left === null && node.right === null) return null;
if(node.left === null) return node.right;
if(node.right === null) return node.left;
if(node.left !==null && node.right !==null){
let _node = this.getMin(node.right);
node.data = _node.data;
node.right = removeNode(node.right,data);
return node
}
} else if(data < node.data){
node.left=removeNode(node.left,data);
return node
} else {
node.right=removeNode(node.right,data);
return node
}
};
return removeNode(this.root,data)
}
}
//创建BST
const tree = new BinarySearchTree();
tree.insert(11);
tree.insert(7);
tree.insert(5);
tree.insert(3);
tree.insert(9);
tree.insert(8);
tree.insert(10);
tree.insert(13);
tree.insert(12);
tree.insert(14);
tree.insert(20);
tree.insert(18);
tree.insert(25);
console.log(tree);
console.log(tree.root);
//中序遍历BST
console.log(tree.inOrder());
//前序遍历BST
console.log(tree.preOrder());
//后序遍历BST
console.log(tree.postOrder());
//搜索最小值
console.log(tree.getMin());
//搜索最大值
console.log(tree.getMax());
//查找特定值
console.log(tree.find(2));
console.log(tree.find(3));
console.log(tree.find(20));
//删除节点,返回新的二叉树,不改变原来的二叉树
console.log(tree.remove(11));
a=tree.remove(11);
console.log(a.root);
console.log(tree);本文内容仅供个人学习、研究或参考使用,不构成任何形式的决策建议、专业指导或法律依据。未经授权,禁止任何单位或个人以商业售卖、虚假宣传、侵权传播等非学习研究目的使用本文内容。如需分享或转载,请保留原文来源信息,不得篡改、删减内容或侵犯相关权益。感谢您的理解与支持!


